Lógica formal

Te explicamos en qué consiste esta lógica que se aplica en filosofía, matemáticas y ciencia y cuál es su función. Además, ejemplos de las tablas de verdad y más.

¿Qué es la lógica formal?

La lógica formal o lógica matemática es la lógica que se utiliza en filosofía y que se aplica a las matemáticas y a la ciencia. Su tarea es “traducir” el lenguaje natural al lenguaje lógico. Por ejemplo, si se toma la oración del lenguaje natural “Está lloviendo y la calle está mojada”, la lógica formal tiene que traducir la información al lenguaje lógico (en este caso: “p ∧ q”).

Para representar el lenguaje natural en lenguaje lógico, la lógica formal utiliza símbolos lógicos. Existen distintos sistemas formales de representación. Los más utilizados son el sistema de lógica proposicional, el de lógica del primer orden y el de lógica modal. Cada uno de estos sistemas opera sobre distintos elementos (proposiciones, predicados y valores de verdad) y variables (proposicionales, cuantificadores y de individuo).

La lógica formal engloba cuatro áreas fundamentales que exploran diferentes aspectos de la matemática y la lógica:

• Teoría de modelos. Es el análisis de estructuras. En esta disciplina se investiga el estudio de teorías axiomáticas y lógica matemática mediante el análisis de estructuras matemáticas complejas, como conjuntos, redes o sistemas dinámicos. Esto permite atribuir un contenido semántico a las construcciones formales de la lógica y comprender su significado en un contexto matemático más amplio.
• Teoría de la demostración. Es la investigación de métodos de validación. En esta área se busca desarrollar métodos y técnicas para la validación de problemas lógicos y la demostración de teoremas mediante el uso de herramientas matemáticas avanzadas. Estos métodos son fundamentales para garantizar la solidez y confiabilidad de los razonamientos lógicos y matemáticos.
• Teoría de conjuntos. Es la exploración de conjuntos y relaciones. Esta rama de la lógica se centra en el estudio de conjuntos y sus interrelaciones, así como en las propiedades y operaciones básicas asociadas. El análisis riguroso de conjuntos proporciona una base sólida para el desarrollo de teorías matemáticas y es esencial en múltiples áreas de la matemática y la lógica.
• Teoría de computabilidad. Es la conexión entre matemática e informática. En esta área de investigación se examina la relación entre la matemática y la informática, especialmente en lo que respecta a los problemas de decisión y la computabilidad. Se estudia cómo los algoritmos y las máquinas de cálculo pueden enfrentar y resolver problemas lógicos y matemáticos complejos, lo que implica la comprensión de conjuntos computables y no computables.

Estas cuatro áreas de la lógica formal abren un vasto campo de investigación y aplicación en el que se exploran diversos aspectos de la matemática, la lógica y su conexión con la informática.

• Ver además: Lógica

Lógica proposicional

La lógica proposicional trabaja con proposiciones lógicas. Cada proposición lógica se simboliza con una letra minúscula y posee un valor de verdad (verdadero o falso). Existen proposiciones simples y compuestas. 

Ejemplos de proposiciones lógicas:

• p = Aristóteles es un hombre.
• q = 4 es un número par.
• r = 5 es la suma de 3 y 2.
• s = La lluvia sale de la tierra.
• t = Juan es mexicano y María española.

En los ejemplos proporcionados, p, q, r y s son casos de proposiciones simples, mientras que t es una proposición compuesta. Además, de las primeras tres se puede decir que son proposiciones verdaderas, mientras que s es una proposición falsa.

Conectivas lógicas

Las proposiciones compuestas están formadas por más de una proposición simple, reunidas a través de conectivas lógicas. En el caso de t, se muestra la unión de dos proposiciones simples: “Juan es mexicano” y “María es española”, unidas por la conectiva lógica “y”, que se llama “conjunción”.

Existen otras conectivas lógicas, como la negación, la disyunción, la condición material y el bicondicional. Todas ellas se simbolizan mediante un signo propio:

• Negación (no): ¬
• Conjunción lógica (y): ∧
• Disyunción lógica (o): ∨
  Tiene dos significados diferentes: 
  Inclusivo. Para que la proposición sea cierta, tiene que ser verdadero uno o todos los elementos de la premisa.
  Exclusivo. En una premisa, “p o q” es verdadero, pero no puede darse el caso en que ambos puedan serlo en simultáneo.

• Condicional material (Si... entonces): →
• Bicondicional (si y solo si): ↔

Las conectivas lógicas se utilizan en el lenguaje formal de la lógica proposicional. Cumplen la función de negar una proposición o poner en relación dos o más proposiciones. 

A continuación, un ejemplo de una oración del lenguaje natural llevada al lenguaje de la lógica proposicional, en la que se da el caso de una conjunción:

• Está lloviendo y la calle está mojada.
• p ∧ q

Tablas de verdad

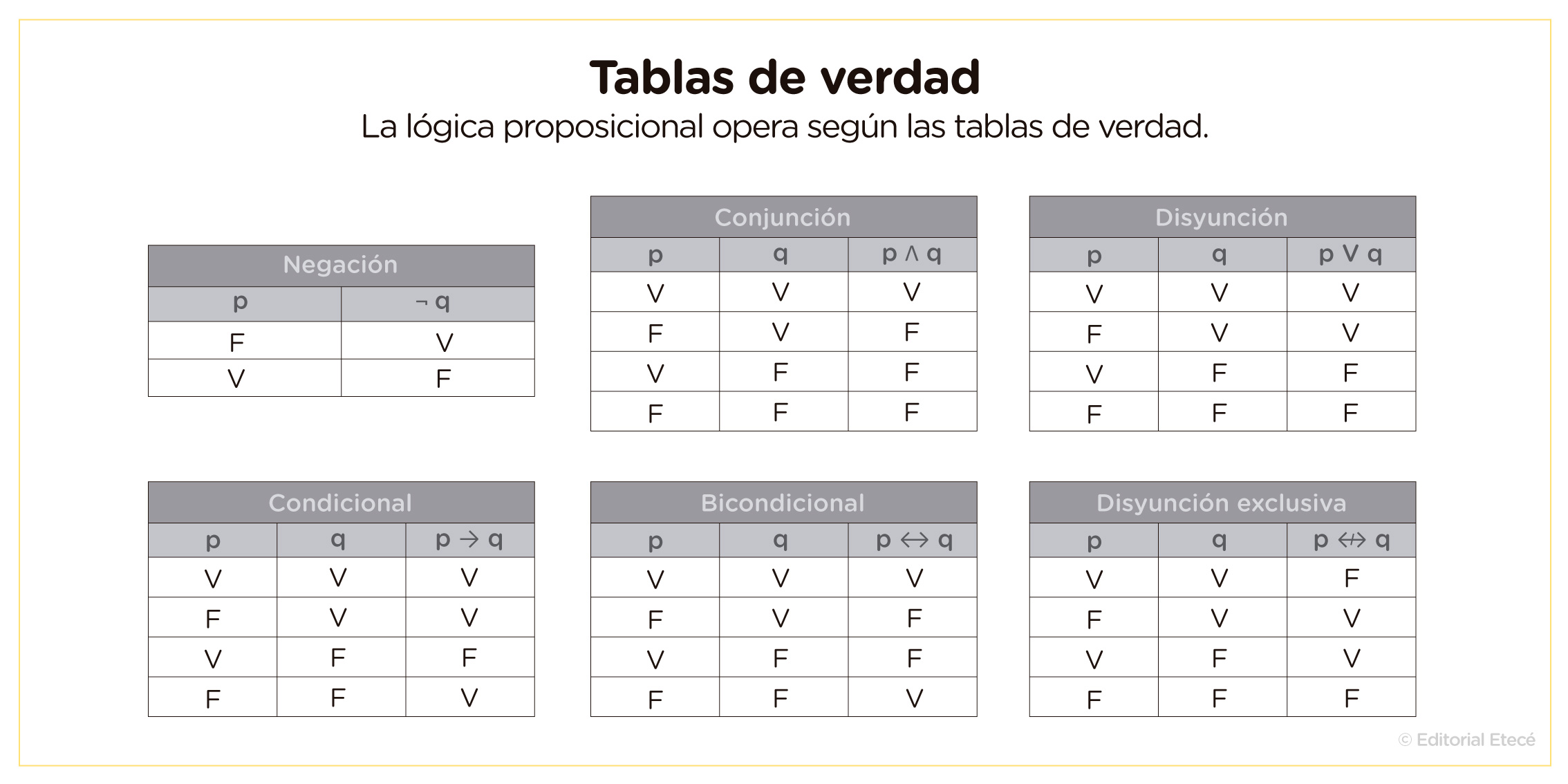
Además de las conectivas lógicas, la lógica proposicional opera según las tablas de verdad. Si cada premisa adquiere un valor de verdad (verdadero o falso), al poner dos o más premisas en relación, el valor de verdad que cada una tenga asignado hará variar el valor de verdad que se le deba asignar a la relación establecida entre ambas.

Así, el significado de cada conectiva lógica puede mostrarse a través de las tablas de verdad que las representan: negación, conjunción, disyunción, condicional, bicondicional y disyunción exclusiva.

Ejemplos de lógica proposicional

• Juan fue al río y María también.
  p: Juan fue al río
  q: María fue al río
  p∧q
• Juan fue al río o María fue al río.
  p: Juan fue al río
  q: María fue al río
  p∨q
• Juan fue al río solo si María fue al río.
  p: Juan fue al río
  q: María fue al río
  p↔q
• Si Juan fue al río, María fue al río.
  p: Juan fue al río
  q: María fue al río
  p→q

Lógica de primer orden

La lógica de primer orden o lógica de predicados trabaja con lenguajes de primer orden. Los lenguajes de primer orden son lenguajes formales que operan con predicados que operan con argumentos que son solo constantes o variables de individuos, y cuantificadores que alcanzan a variables de individuo.

Predicados 

Un predicado es una expresión lingüística que, conectada a otra expresión, forma una oración. Por ejemplo, cuando se afirma “El agua moja”, la expresión “moja” es un predicado que se conecta con la expresión “El agua”. Puede ser que se dé el caso de un predicado que se conecte a dos o más expresiones, como en “El agua moja más que la tierra”.

Cuando un predicado se conecta a una sola expresión, se dice que expresa una propiedad (en este caso, la propiedad de mojar). Cuando se conecta a dos o más, se dice que expresa una relación (en el segundo caso, la relación de mojar más que).

En la lógica de primer orden o lógica de predicados, a los predicados se los trata como funciones. Las funciones toman expresiones como “agua” o “tierra” y las trasforma de la siguiente manera:

• “El agua moja”
  Mojar (Agua)
  M(a)
• “El agua moja más que la tierra”
  Mojar (agua, tierra)
  M(a, t)

Constantes y variables individuales

Las constantes individuales son expresiones lingüísticas que refieren a una entidad. Por ejemplo “agua” o “tierra” son constantes del individuo. Por otro lado, las variables individuales no tienen una referencia determinada, sino que pueden adjudicarse a cualquier entidad. Esto se ejemplifica al decir “esto moja”, y se escribe:

• M(x)

Ya que no se aclara a qué se refiere con la expresión “esto”. Además, las variables, como las constantes, sirven para formalizar oraciones. Por ejemplo, si decimos “Esto moja más que aquello”, y adjudicamos a “esto” la x y a “aquello” la y, podemos simbolizar así:

• M(x,y)

Cuantificadores

Los cuantificadores son operadores que actúan sobre un conjunto de individuos. Es un recurso que permite construir proposiciones que afirman que una condición se cumple para un número determinado de individuos. Los cuantificadores más utilizados son el cuantificador universal y el cuantificador existencial.

• Cuantificador universal. Afirma que una condición se cumple para todos los individuos de los que se está hablando.
  La expresión “para todo x” es un cuantificador universal que se escribe de la siguiente manera: ∀x. 
  Cuando se la utiliza en un predicado, por ejemplo, “para todo x, x está mojado”, se escribe: ∀x M(x). Nótese que en este caso la “M” es la variable que representa la condición de estar mojado.
• Cuantificador existencial. Afirma que una condición se cumple para al menos uno de los individuos de los que se está hablando.
  La expresión “existe al menos un x” es un cuantificador existencial que se escribe de la siguiente manera: ∃x. 
  Cuando se la utiliza en un predicado, por ejemplo, “existe al menos un x, tal que x está mojado”, se escribe: ∃x M(x). Nótese que en este caso la “M” es la variable que representa la condición de estar mojado.

Lógica modal

La lógica modal trabaja sobre el valor de verdad de las distintas proposiciones y predicados. Es la lógica que se encarga de estudiar las formas en que las distintas proposiciones y predicados pueden ser falsos o verdaderos.

Esto sucede porque, si bien es cierto que los predicados y las proposiciones son o bien falsos o bien verdaderos, también sucede que no lo son siempre del mismo modo. Cuando se habla de verdad y falsedad, se habla de necesidad, posibilidad, contingencia e imposibilidad. 

Cada una de las modalidades expresa una forma en que una verdad o una falsedad se manifiestan. Por ejemplo, si se afirma que “Sócrates murió en un combate cuerpo a cuerpo”, la afirmación es falsa pero posible. En cambio, al decir que “2+2=5”, la falsedad de la proposición es necesaria ya que 2 +2 nunca puede ser igual a 5.

Sigue con:

• Filosofía
• Ramas de la filosofía
• Argumento inductivo
• Argumento deductivo
• Historia de la filosofía

Referencias

• Gamut, L. T. F., & Durán, C. (2002). Introducción a la lógica. Buenos Aires, Argentina: Eudeba.
• Obiols, G. (1997). Nuevo curso de Lógica y Filosofía. Kapelusz.
• Díez, J. A. (2002). Iniciación a la Lógica. Ariel.