Teorema de Pitágoras

Te explicamos qué es el teorema de Pitágoras, cómo es su formula y explicación. Además, cuáles son sus características, usos y ejemplos.

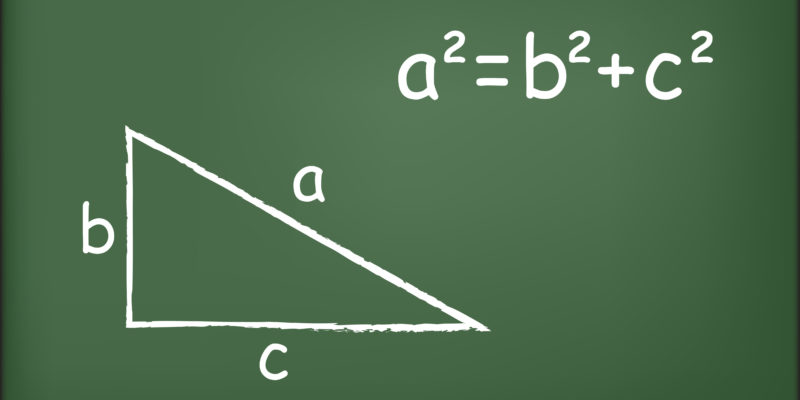
¿Qué es el Teorema de Pitágoras?

El Teorema de Pitágoras es un postulado matemático hecho por el filósofo y matemático griego Pitágoras de Salmos (c. 569 – c. 475 a. C.), estudioso de las leyes de la matemática cuyos aportes a la aritmética y la geometría persisten hasta hoy en día. Este postulado reza que la suma del cuadrado de los catetos de un triángulo rectángulo es siempre igual al cuadrado de su hipotenusa.

Esta proposición es, sin dudas, una de las más conocidas de la historia de la matemática, y la que cuenta con el mayor número de demostraciones a lo largo de los tiempos, a través de diferentes métodos y elaboradas por diversos filósofos y matemáticos.

Según algunos autores se pueden hallar hasta mil demostraciones diferentes, aunque se han catalogado formalmente 367. Esto se debe a que la demostración del teorema era requisito durante la Edad Media para alcanzar el título de Magíster matheseos (“Maestro de matemáticas”) en la academia.

Historia del Teorema de Pitágoras

Si bien se atribuye la autoría del teorema al griego Pitágoras, pues su demostración era de importancia capital para los filósofos pitagóricos (discípulos formados en un culto casi religioso de la matemática), la verdad es que el origen de este teorema es muy anterior.

Existen evidencias de su uso en tablillas babilónicas y papiros del Antiguo Egipto, pero ningún documento que exponga su relación se conserva hasta hoy. Es sabido que el estudio de los triángulos era central en muchas de las culturas antiguas.

Preceptos básicos del Teorema de Pitágoras

Para empezar con el teorema de Pitágoras debe entenderse que se llama catetos a los lados de un triángulo rectángulo que forman el ángulo recto (de 90°) y se llama hipotenusa al lado restante y más largo.

Fórmula del Teorema de Pitágoras

El teorema de Pitágoras se formula de la siguiente manera: a² + b² = c² donde a y b son los catetos de un triángulo rectángulo y donde c es su hipotenusa. De esta formulación se derivan tres corolarios o formulaciones posteriores, de aplicación práctica y verificación algebraica:

• a = √c² – b² (a es igual a la raíz cuadrada de c al cuadrado menos b al cuadrado)
• b = √c² – a² (b es igual a la raíz cuadrada de c al cuadrado menos a al cuadrado)
• c = √a² + b² (c es igual a la raíz cuadrada de a al cuadrado más b al cuadrado)

Explicación del Teorema de Pitágoras

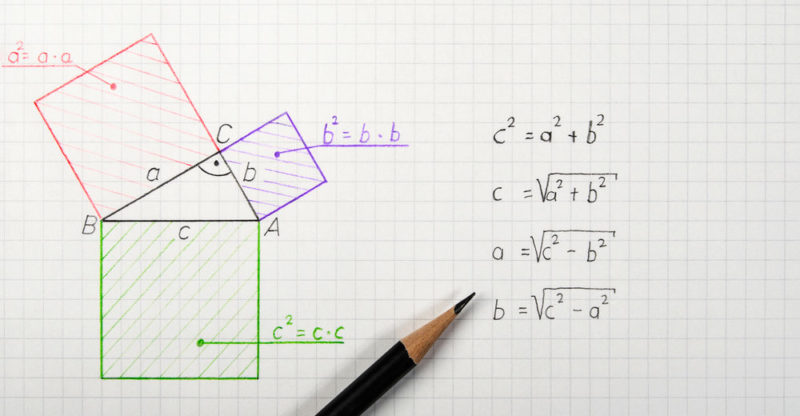
La lógica del teorema de Pitágoras es bastante simple y evidente. Dado un triángulo de lados a, b y c, en el que a y b forman un ángulo recto (es decir, de 90°), es posible calcular la longitud de la hipotenusa sumando los cuadrados de los catetos o, cualquiera de los lados del triángulo.

Ejemplo del Teorema de Pitágoras

Un ejemplo sencillo de la aplicación del teorema es el siguiente:

• Dado un triángulo rectángulo cuyos catetos a y b miden 3 y 4 cm respectivamente, podremos calcular su hipotenusa c sustituyendo los valores en la fórmula, de la siguiente manera:

c² = a² + b²

luego c² = 3² + 4²

y por ende c² = 9 + 16 = 25

y finalmente c = √25 = 5

La hipotenusa c mide 5 cm

Demostraciones del Teorema de Pitágoras

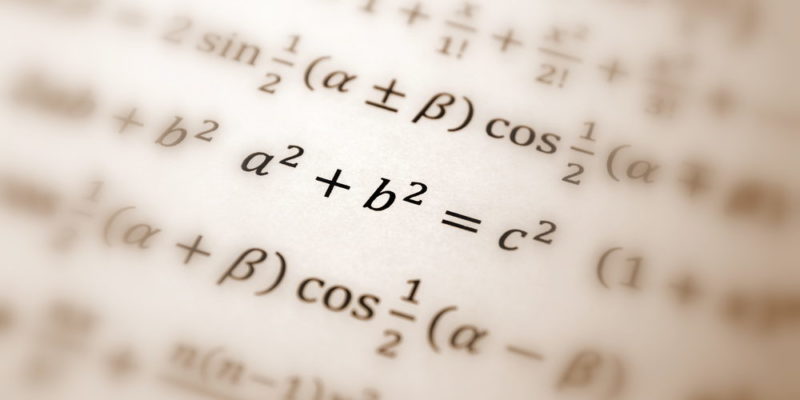
Las demostraciones del teorema de Pitágoras son tan variadas como numerosas, pero se destacan las propuestas por Euclides (325-265 a.C.), Pappus de Alejandría (290-350 a.C.), Bhaskara II de la India (114-1185 d.C.), Leonardo da Vinci (1452-1519 d.C.) y James Garfield (1831-1881).

Cada uno empleó métodos geométricos y aritméticos distintos que, no obstante, condujeron siempre a la misma confirmación del teorema.

Demostración recíproca del Teorema de Pitágoras

Es posible emplear este teorema en su sentido inverso, para comprobar si un triángulo dado es rectángulo (en los casos, por ejemplo, en que no se lo pueda graficar).

Esto es sumamente sencillo: si en un triángulo cualquiera resulta ser cierto que la suma del cuadrado de sus catetos es igual al cuadrado de la hipotenusa, entonces necesariamente los dos primeros formarán un ángulo recto y estaremos en presencia de un triángulo rectángulo.

Aplicaciones del Teorema de Pitágoras

Las aplicaciones de este teorema son numerosas en el campo de la ingeniería, la arquitectura y de la geometría en general. Desde tiempos antiguos el estudio del triángulo con fines prácticos rindió frutos tangibles, como son las famosas pirámides de Egipto.

Cualquier situación de cálculo en la que se esté en presencia de un triángulo rectángulo permitirá la aplicación de este teorema para calcular cualquiera de sus lados.

Importancia para otras áreas

Otras áreas de la matemática pueden servirse de este teorema para sus cálculos. Por ejemplo:

• La geometría analítica plana. Se utiliza este teorema para hallar la distancia entre puntos de un plano cartesiano.
• La trigonometría. Se utiliza este teorema para demostrar la identidad fundamental  sen2^a + cos2^a= 1.

Ejercicios sobre el Teorema de Pitágoras

A continuación se presentan dos ejercicios al respecto:

• Dada la hipotenusa de 20 cm en un triángulo rectángulo del cual se sabe además que uno de sus catetos mide 5 cm, ¿Cuánto medirá el cateto restante?
• Si se necesita hacer una rampa en un peldaño de una escalera y se sabe que el alto del peldaño es de 30 cm y el largo del peldaño es de 1 m, ¿Cuánto deberá medir el plano inclinado de la rampa?

Sigue con: Polígonos