Cuadriláteros

Te explicamos qué es un cuadrilátero y cómo se clasifica este polígono. Además, cuáles son sus características principales y algunos ejemplos.

¿Qué son los cuadriláteros?

Los cuadriláteros son polígonos (figuras geométricas planas) de cuatro lados y dos diagonales. Se caracterizan por tener cuatro vértices y cuatro ángulos, y la suma de sus ángulos internos siempre es de 360°. Por ejemplo: un cuadrado, un trapecio o un rombo.

Estas figuras son también conocidas como cuadrángulos y son usadas en disciplinas como la geometría. La palabra cuadrilátero deriva del latín, de los términos quadri (cuatro) y latus (lados).

Ver además: Teorema de Pitágoras

Características de los cuadriláteros

Algunas de las principales características de los cuadriláteros son:

• Son polígonos, es decir, figuras geométricas cerradas y planas formadas por lados y vértices.
• Pueden ser simples o complejos y en todos los casos tienen cuatro lados y cuatro vértices.
• Pueden tener distintas formas y siempre tienen dos diagonales.
• Tienen cuatro ángulos externos y cuatro ángulos internos (que suman 360°).
• Se clasifican según la suma de sus ángulos interiores en cóncavos y convexos.
• Según el paralelismo de sus lados pueden ser: paralelogramos, trapecios o trapezoides.

Elementos de los cuadriláteros

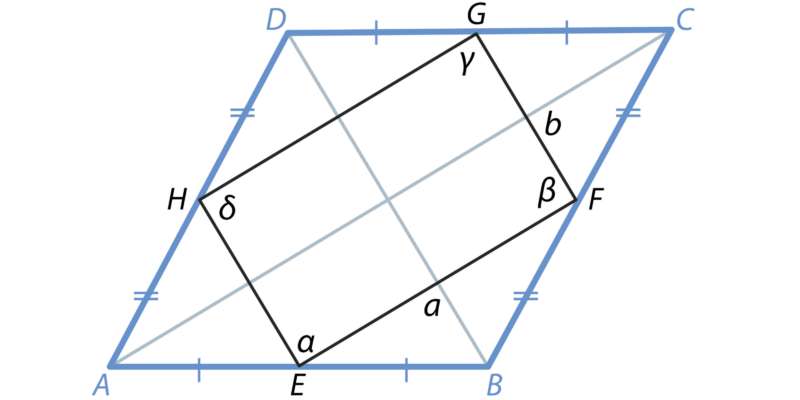
Los cuadriláteros se caracterizan por tener los siguientes elementos:

• Lados. Son líneas o segmentos que se unen a los vértices y que pueden o no ser iguales entre sí.
• Vértices. Son los puntos de intersección de los lados. Cada cuadrilátero tiene cuatro vértices.
• Diagonales. Son segmentos que conectan vértices opuestos.
• Ángulos interiores. Son los ángulos visibles que están determinados por los lados que los conforman. Los ángulos interiores de un cuadrilátero suman 360°.
• Ángulos exteriores. Son los ángulos que se forman con líneas (lados) imaginarias que continúan las líneas del cuadrilátero.

Tipos de cuadrilátero

Los cuadriláteros se pueden clasificar según su forma en cuadriláteros complejos y cuadriláteros simples.

• Cuadriláteros complejos. Son aquellos en los que dos de sus lados se cruzan.
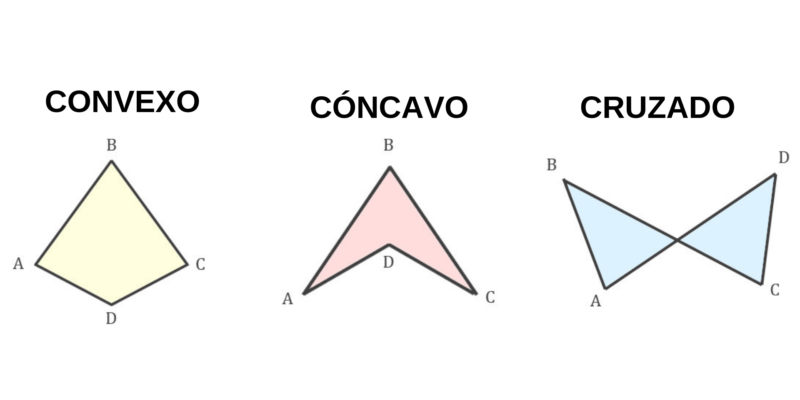
• Cuadriláteros simples. Son aquellos en los que sus lados no se cruzan y pueden ser:
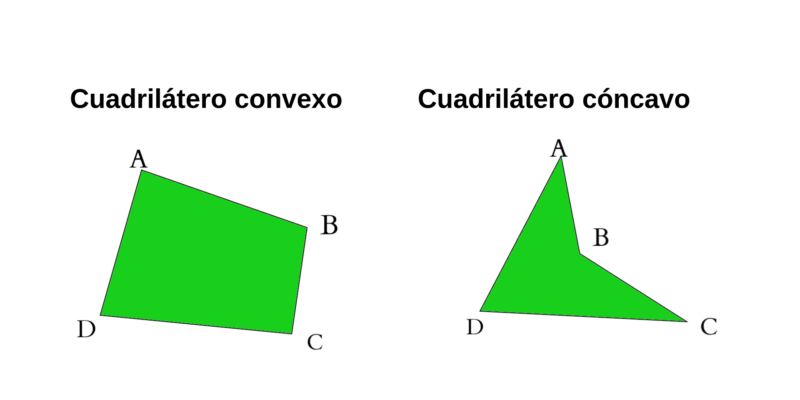
  • Cuadriláteros cóncavos. Son cuadriláteros que tienen algún ángulo que mide más de 180°.
  • Cuadriláteros convexos. Son cuadriláteros que no tienen ningún ángulo interno que mide 180° o más.
  • Cuadriláteros cruzados. Son cuadriláteros que tienen lados que se cruzan o se cortan.

Los cuadriláteros convexos pueden ser:

1. Paralelogramos

Son cuadriláteros que tienen dos pares de lados paralelos y los lados opuestos son idénticos entre sí. También los ángulos internos opuestos son iguales entre sí y las diagonales se cortan en su punto medio. Algunos ejemplos son:

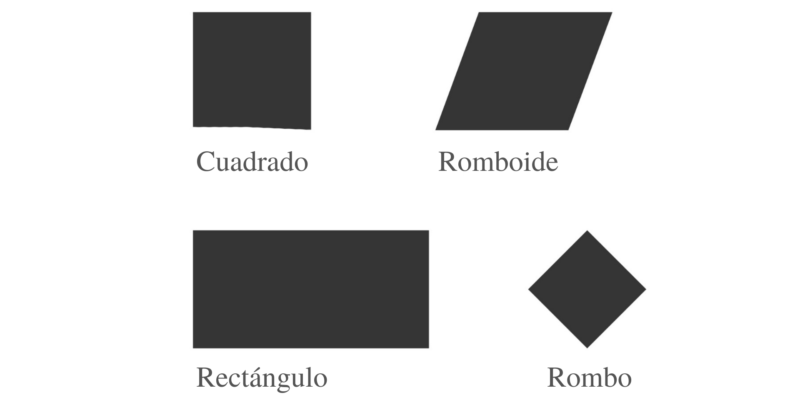
• Romboide. Cuadrilátero que tiene cuatro lados que no forman ángulos rectos y los lados que son opuestos entre sí son iguales.
• Rombo. Cuadrilátero que tiene cuatro lados iguales pero que no forman ángulos rectos.
• Rectángulo. Cuadrilátero que tiene cuatro lados y cada par de lados paralelos miden lo mismo. Al igual que los cuadrados tienen cuatro ángulos rectos.
• Cuadrado. Cuadrilátero con cuatro lados iguales y cuatro ángulos rectos.

2. Trapecios

Son cuadriláteros que tienen dos lados paralelos, que se llaman base mayor y base menor. Los trapecios pueden ser:

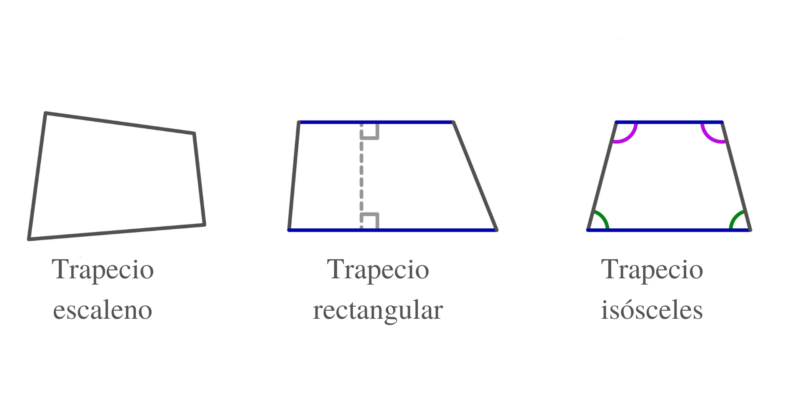
• Trapecio escaleno. Tiene sus cuatro ángulos internos desiguales.
• Trapecio isósceles. Tiene los lados no paralelos iguales.
• Trapecio rectangular. Tiene dos ángulos internos rectos y dos que no son rectos.

Más en: Trapecio

1. Trapezoides

Son cuadriláteros que no tienen ninguno de sus lados paralelos entre sí. Se dividen en:

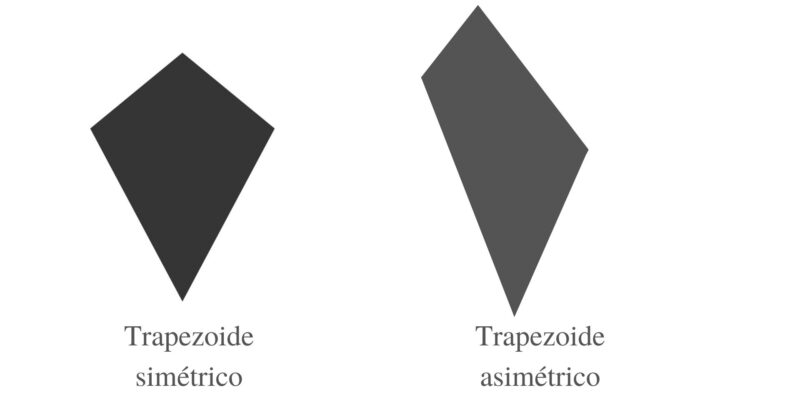
• Trapezoides simétricos. Tienen un eje de simetría interno
• Trapezoides asimétricos o amorfo. No tienen un eje de simetría interno.

Referencias:

• “Quadrilaterals” en Khan Academy.
• “Shape: quadrilateral” en Elementary Math.
• “Cuadriláteros” en Wikipedia.
• “Angles, lines and polygons” en BBC.